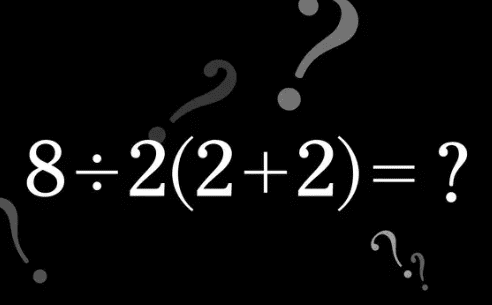Math can be divisive, particularly among high school students who believe they won’t ever need it when they graduate. Because of the memorization required to remember the rules and formulas or the precise calculations necessary—after all, one errant decimal point might result in numerous errors—kids may occasionally dread their mathematics session.
But, whether you realise it or not, mathematical equations are used in almost every aspect of your life, from cooking and construction to the forecast for tomorrow. Even internet security and assessing the number of people at danger in the case of a natural disaster use it.
Trigonometry, calculus, algebra, geometry, and statistics are a few of the most widely used fields of mathematics. Equations that can be used to explore and even build the world for the benefit of humanity are derived from these fields of research.
The Pythagorean Theorem in Architecture
A fundamental mathematical formula ( Just like 1dwycrh5dihrm96ma5degs2hcsds16guxq) known as the Pythagorean theorem was developed by the Greek mathematician Pythagoras. The Pythagorean Theorem functions as follows: The hypotenuse, or side on the other side of the 90-degree angle, of a triangle, is equal to the sum of the squares of the other two sides. The Pythagorean theorem is frequently applied in architectural design and has a wide range of useful, real-world applications. It is visible in the houses, buildings, ramps, and bridges. For instance, dwellings can be designed with sloped roofs that have a 90-degree angle at the top using right triangles and the Pythagorean theorem.
Determining force for space and aircraft travel using the sine and cosine functions
The sine and cosine functions were probably covered in a precalculus class in high school. In their simplest terms, sine and cosine are mathematical equations that determine the size, shape, and angle of a right triangle. Aerospace engineers at organisations like NASA employ the functionalities because they are crucial to both space and aeroplane trips. One option for orbiting the Planet is to employ a space shuttle. To do this, scientists must compute the orbit curve of the shuttle in relation to the equator of the planet, resulting in an orbit curve that resembles a sine curve.
logogriphs for pH measurement
Back in high school chemistry, you might recall dipping tiny strips of paper into chemicals and monitoring whether the paper became a different colour. You were probably testing the acidity of an item or solution or determining the pH scale in these situations. You must use logarithms in your equations to accomplish this. A logarithm is the power to which a number must be raised in order to change its value. It’s crucial to measure pH when determining how acidic commonplace materials like water and soil are. To ensure that household items like cleaners, dishwashing detergent, toothpaste, and skincare products are safe and effective, chemists must also maintain the proper pH balance.
Equations of probability for disaster risk
Probabilistic equations are similar to how they sound—mathematical equations used to forecast the possibility of an event. When assessing the risk of a calamity, probability equations are quite useful. The Office of Disaster Preparedness and Management, for instance, multiplies the “probability of hazard” by the level of vulnerability when calculating risk. Scientists would conduct a disaster risk assessment using probability equations if a natural disaster, like a hurricane, was predicted to affect a specific region to determine the possible liability and loss of property and even human life. Scientists consider acceptable risk and residual risk, which are risk categories that refer to risk that is considered manageable and risk that is still possible even in the presence of preventive measures.
The exponential growth and demise of microorganisms
If you ever took biology in high school, you might recall hearing about exponential functions. The population growth over time can be calculated using this equation. In biological studies, exponential functions are frequently used to quantify bacterial growth and decay. As an illustration, if a bacterial cell divides into two and then each of those two cells divides into two, you will soon have bacteria cells in groups of four, eight, sixteen, thirty-two, and so on. Science needs to employ exponential functions because they may be used to monitor the expansion of viruses and diseases.
Cryptology using the Fibonacci sequence
For instance, the Fibonacci series would seem as follows if you began with the number zero: 0 is followed by 1, 2, 3, 5, 8, 13, and so on. The Fibonacci sequence is renowned for appearing in nature; it is followed by the growth of the leaves and petals of trees, flowers, and other naturally occurring spiral patterns. It is also extremely helpful in the field of cryptology, which is the study of codes and how to break them. The Fibonacci sequence can be utilised in current technology to securely encrypt sensitive data sent over the internet.
Cooking fractions
It’s likely that you’ve used fractions in the kitchen in addition to measuring cups and spoons, whether you’re a chef, baker, or home cook. A fraction is a piece of a whole. For instance, 25% of a whole is equivalent to a quarter, and one-eighth of a whole is equal to a half. When cooking, fractions may be very useful because you may come across recipes that don’t specify how many servings to make or run into other situations where you’ll need to do some quick math. You must accurately split all of your components in half, for instance, if you are cooking for four people but the recipe was designed for eight. Otherwise, you risk having too much food or a dish that doesn’t turn out well because you used too much of an ingredient.